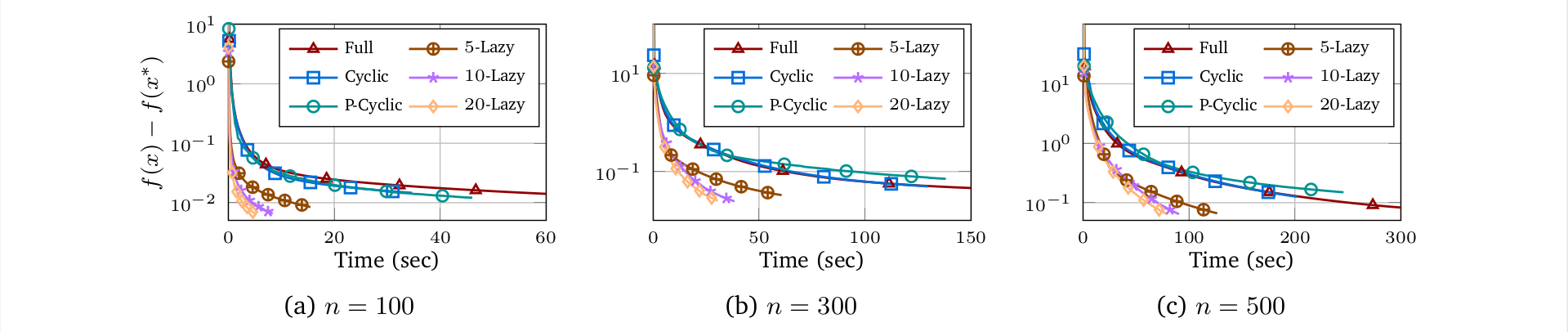
We prove that the block-coordinate Frank-Wolfe (BCFW) algorithm converges with state-of-the-art rates in both convex and nonconvex settings under a very mild “block-iterative” assumption, newly allowing for (I) progress without activating the most-expensive linear minimization oracle(s), LMO(s), at every iteration, (II) parallelized updates that do not require all LMOs, and therefore (III) deterministic parallel update strategies that take into account the numerical cost of the problem’s LMOs. Our results apply for short-step BCFW as well as an adaptive method for convex functions. New relationships between updated coordinates and primal progress are proven, and a favorable speedup is demonstrated using FrankWolfe.jl